As shown in figure 1, suppose a column is under a concentric axial load (compressive load). When the load becomes bigger and bigger, deflection and strain of column also get bigger and bigger. Because of its flexural rigidity, column can bear the load to some extent, but when the load reaches a certain value, column deforms remarkably and almost lose its flexural rigidity. At this point, no more resistance can be expected from the material, which means, failure will occur immediately. This phenomenon is called buckling of material, and the maximum load that column can bear before failure is called buckling load.
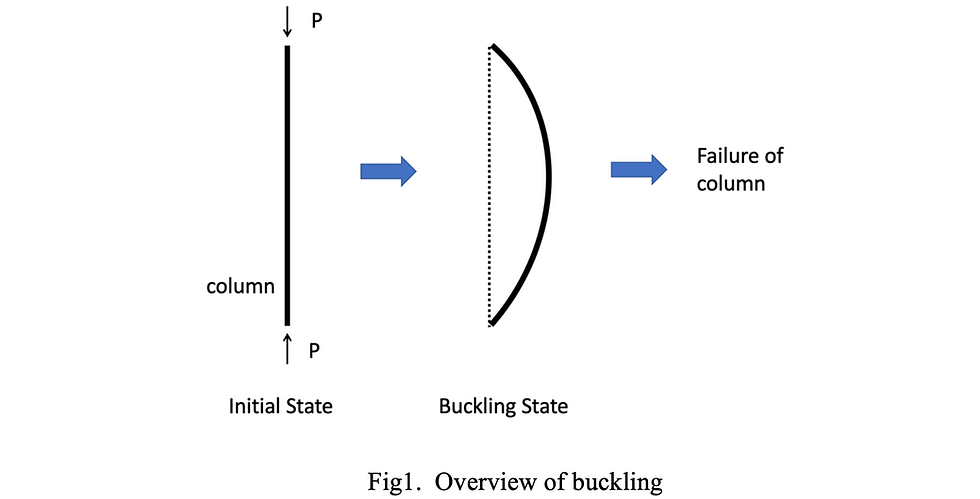
In 1757, a Swiss mathematician, Leonhard Euler studied buckling phenomenon and successfully derived buckling load of material. Since then, buckling load is famously known as Euler’s load or Euler’s critical load.
Following is a sample mathematical derivation of Euler’s critical load.
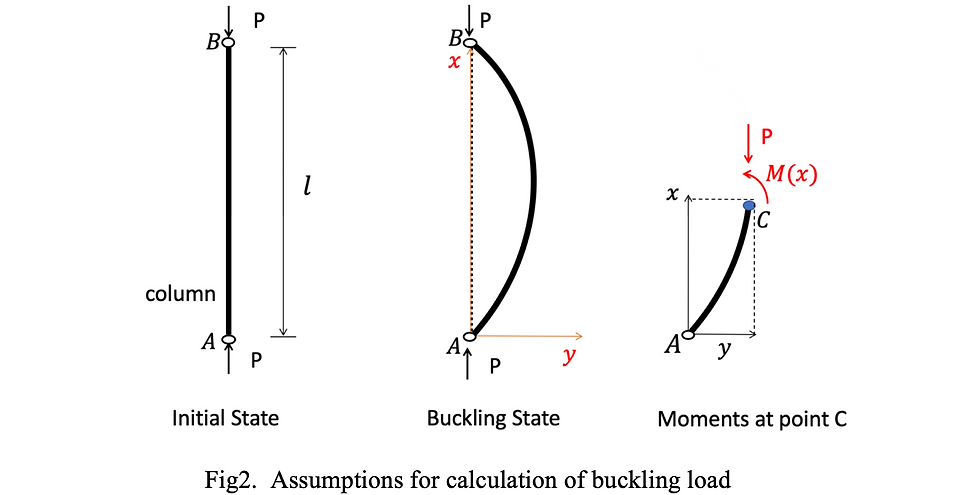
Consider a pin-ended column under the effect of buckling load.
Assumptions:
①. Load P is applied slowly to both ends of column.
②. Suppose a cartesian coordinate (Axy) as shown in figure 2 where x axis matches center of gravity(centroid) of column, y(x) is the deflection of column at distance x
③. At point C(x,y), suppose that buckling occurs.
Since there are no reactions on the hinged end, then there is no shear force at any cross section of the material. Forces acting on the column are only moments as shown on the right side of the figure.
Equilibrium condition of free body by using Newton’s First Law
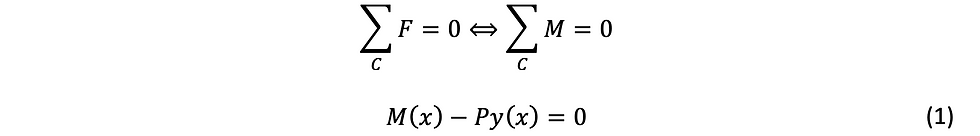
Euler-Bernoulli beam theory (or Elastic curve equation)
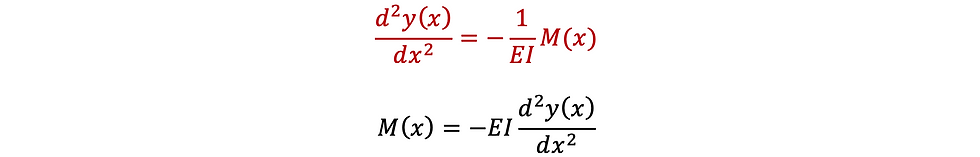
Then equation (1) can be written as
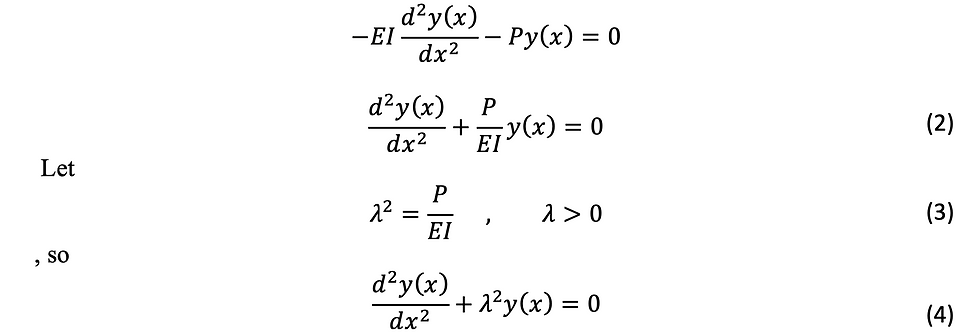
Equation (4) is a homogeneous second-order ordinary differential equation.
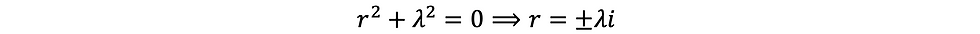
Then general solution of equation (4) is
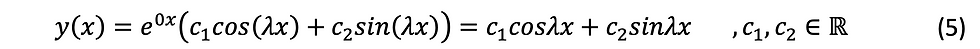
As shown in figure 2 boundary conditions are:
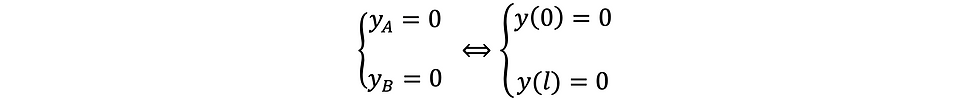
Thus equation (5) can be now be written as
Trivial solution of equation (6) is c1 = c2 = 0 . Then y(x) = 0 , which means there is no effect of buckling load and column stays straight. Therefore, buckling load cannot be derived (nonbuckled state) in this case. Either c1 or c2 must be a real number that not equal to zero. To get this result, determinant of coefficient matrix must equal to zero. This condition is called buckling condition and is written as the following equation (7).
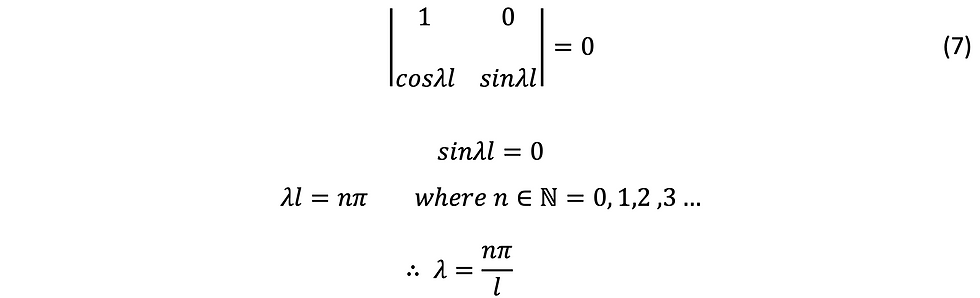
Then equation (3) becomes
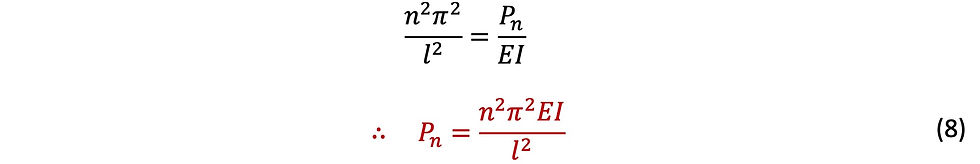
This Pn is called buckling loads.
Substitute λl＝nπ into equation (6)
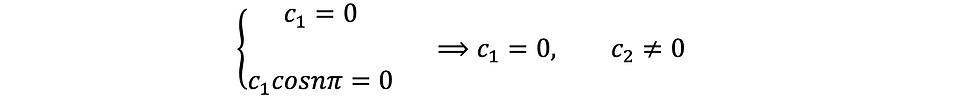
Then equation (5) becomes
This is called buckling modes of column.Therefore, depending upon the value of n, different buckling modes and buckling loads are produced as shown in figure 3 below. The load mode for n = 0 is the nonbuckled mode.Theoretically, any buckling mode is possible, but in the case of a slowly applied load, only the first mode is likely to be produced. Therefore, Euler’s critical load Pcr is defined by
And buckling shape is defined by
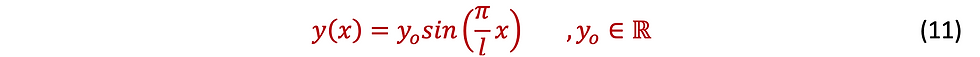
where :
E : Young’s modulus of material
I : Moment of inertia of material
l : Length of material
yo : Maximum deflection of material caused by buckling
REFERENCES
1. 松井千秋：建築鉄骨構造「座屈の基礎―圧縮材の曲げ座屈―」pp 82 - 84,
オーム社，2007
2. Wikipedia. Euler’s Critical Load. 2019
https://en.wikipedia.org/wiki/Euler%27s_critical_load(Accessed 2019. Aug.25th )
Buckling. 2019
https://en.wikipedia.org/wiki/Buckling(Accessed 2019. Aug.25th )
⬇️សម្រាប់ឯកសារជាpdf
វក្យស័ព្ទ
English 日本語 ខេមរភាសា
buckling 座屈 ការភ្លាត់
load 荷重、力 បន្ទុក , កម្លាំង
buckling load 座屈荷重 បន្ទុកភ្លាត់
Euler's load オイラー荷重 បន្ទុកអឺលែ
Euler's critical load オイラー荷重 បន្ទុកអឺលែ
centroid 重心 ទីប្រជុំទម្ងន់
equilibrium condition 釣り合い条件 លក្ខខ័ណ្ឌលំនឹង
free body 自由体
Newton's first law 運動の第１法則 ច្បាប់ទី១ញូតុន
Euler-Bernoulli beam theory オイラー・ベルヌーイの梁の定理 ទ្រឹស្តីបធ្នឹមអឺលែ-ប៉ែនុយយី
Elastic curve equation 弾性曲線方程式 សមីការខ្សែកោងយឺត
nonbuckled state 座屈しない状態 ភាពមិនភ្លាត់
buckling condition 座屈条件 លក្ខខ័ណ្ឌភ្លាត់
buckling mode 座屈モード ម៉ូតភ្លាត់
material 材料 គឿងសំណង់
Young's modulus ヤング率、弾性係数 ម៉ូឌុលយ៉ាំង
Moment of inertia 断面2次モーメント ម៉ូម៉ង់និចលភាព
Comments