កម្មន្ត
- PEN I Uoy

- Jun 11, 2020
- 1 min read
អានុភាព
នៅក្នុងលំហសិក្សា R មានចំណុចរូបធាតុ A ធ្វើចលនាដោយល្បឿន v រងដែនកម្លាំង F ។ តាមនិយមន័យអានុភាព P (Power) នៃដែនកម្លាំងបញ្ចេញលើ A កំណត់ដោយទំនាក់ទំនង ៖

សិក្សាចលនាក្នុងតម្រុយដេកាតគេបានកម្លាំង F កំណត់ដោយ

វ៉ិចទ័រទីតាំងនៃចំណុចរូបធាតុ A កំណត់ដោយ

នោះគេបាន

តាមនិយមន័យផលគុណស្កាលែ

ដូចនេះអានុភាពកំណត់ដោយ
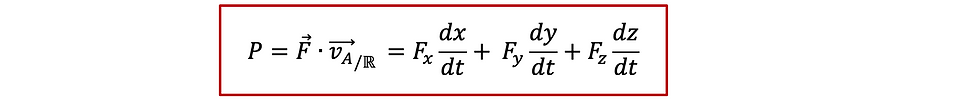
កម្មន្ត
កម្មន្ត W(work) នៃដែនកម្លាំង F (x,y,z) មានអំពើលើចំណុចរូបធាតុ A ណាមួយត្រង់ចំណុច Mi (i=initial) ធ្វើឲ្យវាផ្លាស់ទីទៅចំណុច Mf(final) កំណត់ដោយទំនាក់ទំនង ៖
ទម្រង់ឌីផេរ៉ង់ស្យែល

តាមការបកស្រាយអំពីអានុភាពដូចខាងលើគេបាន
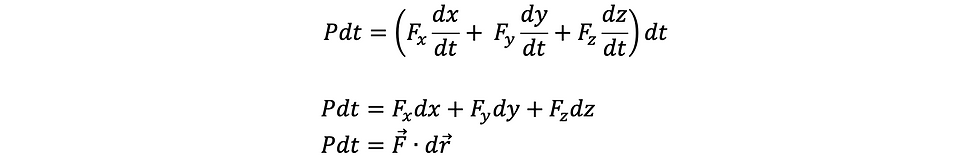
ដូចនេះទម្រង់ឌីផេរ៉ង់ស្យែលនៃកម្មន្តគឺ

ហើយគេបានទម្រង់អាំងតេក្រាលនៃកម្មន្តគឺ

ឧទាហរណ៍១ ក្នុងតម្រុយដេកាតដែនកម្លាំង F មួយកំណត់ដោយ

ចូរគណនាកម្មន្តនៃកម្លាំងនេះមានអំពើលើចំណុចរូបធាតុមួយធ្វើឲ្យវាផ្លាស់ទីតាមគន្លងដែលមានសមីការបារ៉ាមែត្រដូចខាងក្រោម

ចម្លើយ
ទម្រង់អាំងតេក្រាលនៃកម្មន្ត

វ៉ិចទ័រទីតាំងនៃចំណុចរូបធាតុ
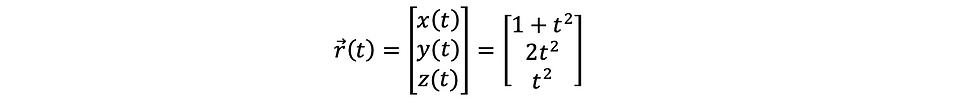
គេបាន

កម្លាំង F អាចធ្វើឲ្យអង្គធាតុផ្លាស់ទីតាមគន្លង (C) បានលុះត្រាតែខ្សែកោង (C) ស្ថិតក្នុងលំហនៃដែនកម្លាំង F ពោលគឺខ្សែដែនកម្លាំង F ពិតជាកាត់តាមខ្សែកោង (C) មែន។
(C) ∈ F ⇔ សមីការខ្សែកោង (C) ផ្ទៀងផ្ទាត់ក្នុងដែនកម្លាំង F
គេបាន
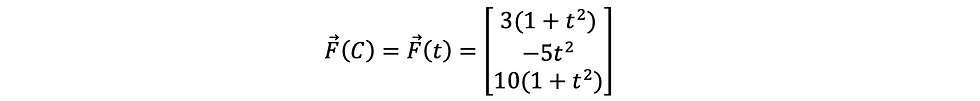
តាមនិយមន័យផលគុណស្កាលែគេបាន

គេបាន

ឧទាហរណ៍២
ចំពោះកម្លាំង F(x,y,z) នៃឧទាហរណ៍ទី១ ចូរគណកម្មន្តប្រសិនបើគន្លង (C) នៃរូបធាតុ A កំណត់ដោយសមីការដូចខាងក្រោម

ចម្លើយ
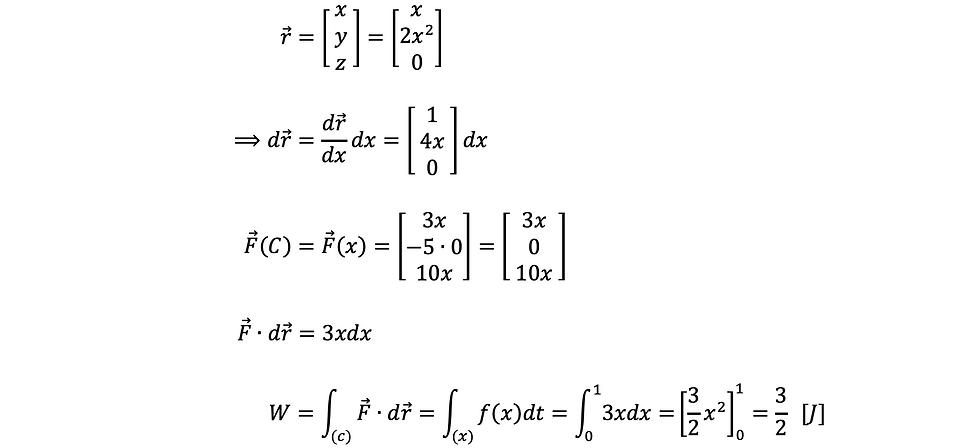




Comments