ថាមពលស៊ីនេទិច (Kinetic Energy)
ថាមពលស៊ីនេទិចEc(Énergie Cinétique)នៃចំណុចរូបធាតុ A មានម៉ាស m ក្នុងតម្រុយសិក្សា R ណាមួយកំណត់ដោយ
ទ្រឹស្តីបទថាមពលស៊ីនេទិច
ក្នុងតម្រុយកាលីឡេ R គេមាន F គឺជាកម្លាំងដែលមានអំពើលើចំណុចរូបធាតុ A មានម៉ាស m ។
ច្បាប់គ្រឹះឌីណាម៉ិច
អានុភាព
ដោយ
នាំឲ្យ
គេបាន
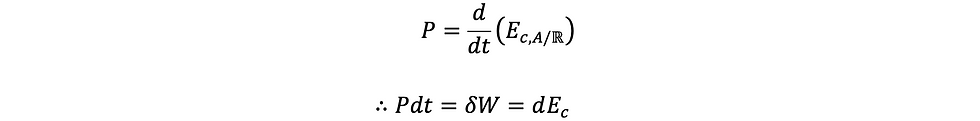
ទ្រឹស្តីបទថាមពលស៊ីនេទិច
ក្នុងតម្រុយកាលីឡេបម្រែបម្រួលថាមពលស៊ីនេទិចនៃរូបធាតុរវាងខណៈពីរគឺជាបម្រែបម្រួលកម្មន្តនៃកម្លាំងដែលបង្កើតឲ្យមានបម្រែបម្រួលនោះ។
កម្លាំងរក្សា
គេថា F គឺជា(ដែន)កម្លាំងរក្សាលុះត្រាតែកម្លាំងនេះអាចទាញចេញពីអនុគមន៍ស្កាលែ (Ep) ណាមួយក្រោមទម្រង់ ៖
អនុគមន៍ស្កាលែ Ep (Énergie Potentielle)ហៅថាប៉ូតង់ស្យែល ឬ សក្តានុពលនៃ F ។ ក្នុងការអនុវត្តជាក់ស្តែង Ep ហៅថាថាមពលប៉ូតង់ស្យែលនៃ F ។
លក្ខណៈនៃកម្លាំងរក្សា
ប្រសិនបើ F គឺជា(ដែន)កម្លាំងរក្សានោះគេបាន
(១) កម្មន្តនៃកម្លាំង F មិនអាស្រ័យនឹងរាងនៃបម្លាស់ទីនោះទេ ពោលគឺវាអាស្រ័យតែលើទីតាំងដើមនិងទីតាំងស្រេចតែប៉ុណ្ណោះ។ ហើយកម្មន្តនេះមានតម្លៃផ្ទុយនឹងបម្រែបម្រួលថាមពលប៉ូតង់ស្យែលរវាងពីរចំណុចនោះ។
ទម្រង់ឌីផេរ៉ងស្យែល
ទម្រង់អាំតេក្រាល
ក្នុងន័យដូចគ្នានេះដែរ ចំពោះករណីគន្លងនៃបម្លាស់ទីជាចលនាវិលវល់(ខ្សែបិទ) ពោលគឺទីតាំងដើមនឹងទីតាំងស្រេចត្រួតគ្នា នោះកម្មន្តនៃកម្លាំងរក្សាស្មើនឹងសូន្យ។
(២)
បំណកស្រាយ
ចំពោះអនុគមន៍ស្កាលែ Ep(x,y,z) ណាមួយក្នុងលំហគេបាន
នាំឲ្យ
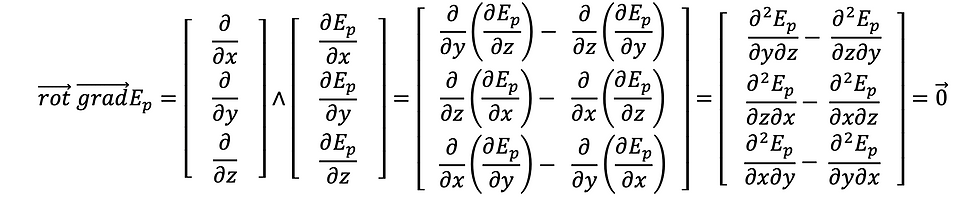
ប្រសិនបើមានដែនកម្លាំង F (x,y,z) ណាមួយផ្ទៀងផ្ទាត់ទំនាក់ទំនង
នោះគេទាញបាន
សញ្ញាដកបញ្ជាក់ថាថាមពលប៉ូតង់ស្យែលថយចុះព្រោះកម្លាំងត្រូវបានបញ្ចេញដើម្បីធ្វើឲ្យចំណុចរូបធាតុផ្លាស់ទីតាមគោលដៅ។
ម្យ៉ាងទៀត
ដូចនេះ
ឧទាហរណ៍ គេមានដែនកម្លាំង F កំណត់ក្នុងតម្រុយ R = OXYZ ចំពោះគ្រប់ចំណុច M(x,y,z) នៃលំហគេបាន
ដែល k ជាចំនួនថេរ។
១- បង្ហាញថា F ជាក្រាដ្យង់នៃថាមពលប៉ូតង់ស្យែលណាមួយ។
២- គណនាកម្មន្តនៃចំណុច M ដែលផ្លាស់ទីពី M1(0,0,0) ទៅ M2(1,1,0) តាមគន្លងនីមួយៗខាងក្រោម៖
ក- M1(0,0,0) → A(1,0,0) → M2(1,1,0)
ខ- សមីការគន្លង
គ- ផ្លាស់ទីដោយសេរី(គ្មានគន្លងកំណត់ច្បាស់លាស់)
ចម្លើយ
១/
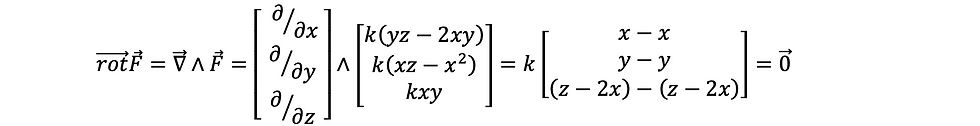
ចំពោះអនុគមន៍ស្កាលែ Ep(x,y,z) ណាមួយក្នុងលំហគេបាន
នាំឲ្យ
ក្នុងកន្សោមនេះ Ep គឺជាថាមពលប៉ូតង់ស្យែលនៃកម្លាំង F ហើយសញ្ញាដកបញ្ជាក់ថាថាមពលប៉ូតង់ស្យែលថយចុះព្រោះកម្លាំងត្រូវបានបញ្ចេញដើម្បីធ្វើឲ្យចំណុចរូបធាតុផ្លាស់ទីតាមគោលដៅ។
២/
ក
ក្នុងចន្លោះ M1 → A គេបានសមីការគន្លងគឺជាបន្ទាត់ y = 0 (z=0)
វ៉ិចទ័រទីតាំងនៃចំណុចរូបធាតុ
នាំឲ្យ
(C) ∈ F ⇔ សមីការខ្សែកោង (C) ផ្ទៀងផ្ទាត់ក្នុងដែនកម្លាំង F
គេបាន
នាំឲ្យ
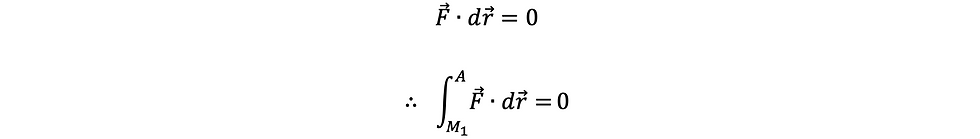
ក្នុងចន្លោះ A → M2 គេបានសមីការគន្លងគឺជាបន្ទាត់ (C) x = 1 (z = 0)
គេបាន
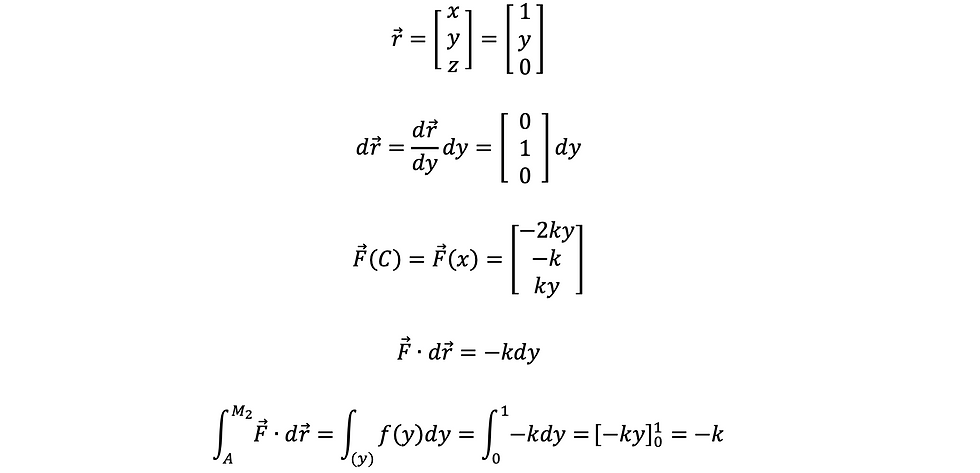
ដូចនេះ
ខ សមីការគន្លង
គេបាន
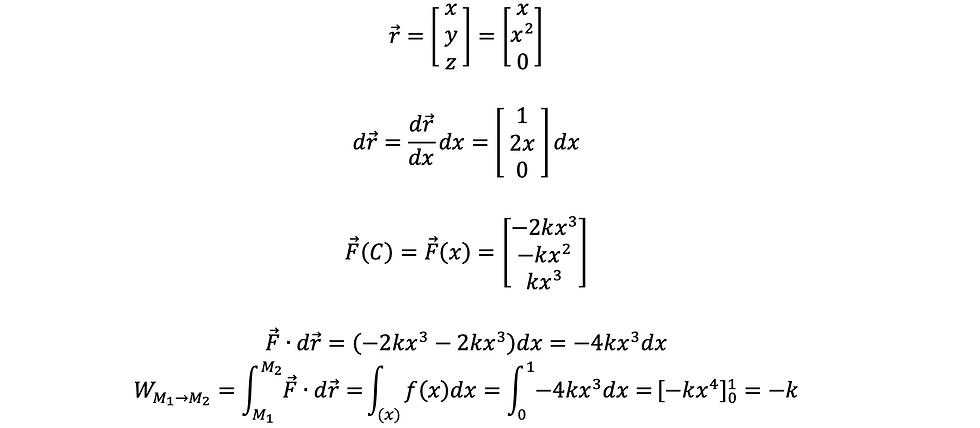
ដូចនេះ
គ- ករណីទូទៅមិនអាស្រ័យនឹងគន្លង
នាំឲ្យ
ផ្ទឹមសមីការ (2)&(5)
នាំឲ្យ
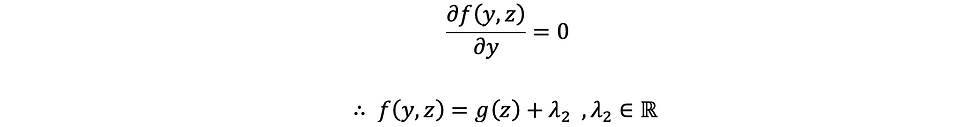
ជំនួសក្នុងសមីការ (2)
នាំឲ្យ
ផ្ទឹមសមីការ (3) & (6)
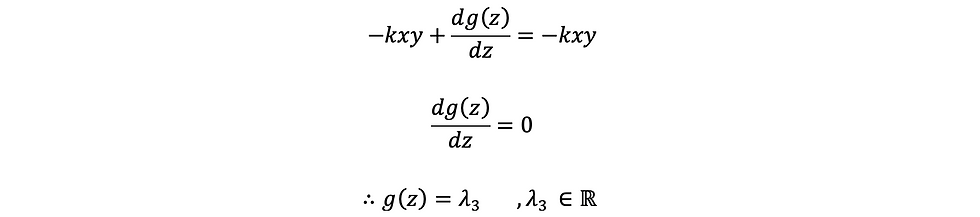
ជំនួសក្នុងសមីការ (4.1)
ឬ
តាមលក្ខណៈនៃកម្លាំងស្កាលែគេបាន
ដែនកំណត់
គេបាន
នាំឲ្យ
ដូចនេះ
ការបកស្រាយក្នុងឧទាហរណ៍នេះបញ្ជាក់លក្ខណៈនានានៃដែនកម្លាំងរក្សា។
កម្លាំងមិនរក្សា
កម្លាំងណាមួយដែលផ្ទៀងផ្ទាត់លក្ខខ័ណ្ឌពីរខាងក្រោមហៅថាកម្លាំងមិនរក្សា
(១) កម្មន្តនៃកម្លាំងដែលមានអំពើលើចំណុចរូបធាតុគឺជាកម្មន្តអវិជ្ជមាន
(២) កម្លាំងនេះមិនអាចទាញចេញពីថាមពលប៉ូតង់ស្យែលណាមួយទេ។
ថាមពលមេកានិច
ថាមពលមេកានិច (Em) នៃចំណុចរូបធាតុគឺជាផលបូកនៃថាមពលស៊ីនេទិចនិងថាមពលប៉ូតង់ស្យែល។
ករណីកម្លាំងរក្សា
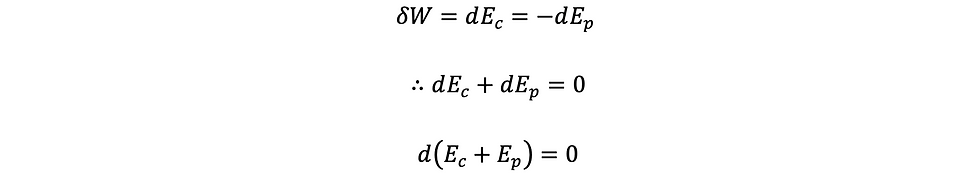
នាំឲ្យ
ពំនោលច្បាប់រក្សាថាមពល
ប្រសិនបើកម្លាំងដែលធ្វើឲ្យអង្គធាតុមានចលនាជាកម្លាំងរក្សា នោះថាមពលមេកានិចរបស់អង្គធាតុមិនបាត់បង់តាមទីតាំងបម្លាស់ទីទេ គឺវាគ្រាន់តែប្តូរប្រភេទថាមពលតែប៉ុណ្ណោះ។
ចំពោះកម្លាំងមិនរក្សា
នៅក្នុងបម្លាស់ទីនៃចំណុចរូបធាតុ ពេលខ្លះប្រភេទកម្លាំងប្រែប្រួលតាមចន្លោះសិក្សា(ទីតាំង)។ ក្នុងករណីនេះថាមពលសរុបនៃចំណុចរូបធាតុគឺជាថាមពលសរុបនៃកម្លាំងនីមួយៗពោលគឺកម្លាំងរក្សា និងកម្លាំងមិនរក្សា។
ថាមពលស៊ីនេទិច
ថាមពលប៉ូតង់ស្យែល
គេបាន
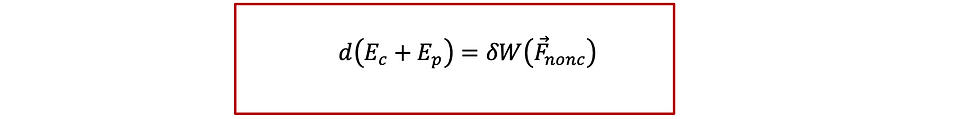
Comments